Euler 15 in Python

This one isn’t even funny…
Starting in the top left corner of a 2×2 grid, there are 6 routes (without backtracking) to the bottom right corner.
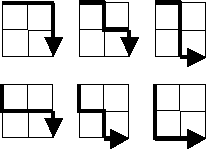
How many routes are there through a 20×20 grid?
Your first thought would be to generate the routes, but for a 20×20 grid, those amount to BILLIONS and you’d try to do it recursively too! Forget it.
But if you have some CompSci-level math background, though, you’ll remember this one—reading The Art of Computer Programming, Vol. 4
[latex size=“3”]frac{(w + h)!}{w!h!}[/latex]
and that’s it. I didn’t even write a program for this, instead using Python’s interactive shell, but just for the same of completeness, here’s a “program” to calculate the possibles paths in a 20×20 grid.
import math
w = h = 20
print math.factorial(w + h) / (math.factorial(w) * math.factorial(h))
That’s it.